Exponential functions are a way to look at the infinite. No human can comprehend how an exponential function grows; if you don’t believe me, here are a few examples.
The first one would be the most famous one: the king who wanted to reward the inventor of chess with anything he desired, so the inventor asked for an exponential amount of rice: one grain on the first square, two on the second, four on the third, eight on the fourth and so on.
The king laughed and sent for a couple bags of rice, but when they calculated the amount of rice, they discovered that halfway through a chessboard of 64 squares there was not enough rice in the kingdom.
Sure you knew this tale and maybe you even feel a little sorry for the king’s naivete.
So let me give you another example: let’s take a walk. How far can 26 paces take you? You guessed it: about 20 meters or 60 feet. Not much, you won’t even get to the next street.
What about 26 exponential paces? The first exponential pace is the same as a normal pace, the second would be two paces, the third would be four paces and so on: same as in the chess tale
I have asked this question to several unsuspecting subjects. The farthest they have estimated is one kilometer (half a mile). Try asking it.
Well, the answer is roughly the circumference of Earth. 26 measly paces can take you from the city of Alexandria to, well, the city of Alexandria but visiting everything in between.
Let’s put it another way. Distance from Earth to Moon? 29 paces. The solar system radius? 52 paces! Distance from the Sun to Alpha Centauri? 55 paces!
The whole Milky Way? Shy of 70 paces.
Ok, I’m going to throw everything I have. And I mean everything.
The radius of the observable universe. All of the 46.508 billion light years. That must be something, right?
Not even 100 paces. Less paces than our smartwatch records on a lazy, lazy day.
Are you feeling closer to the infinite yet?
(If you don’t, you’re right, because we are exactly at the same distance as when we gave the first pace, but that’s something for another post). Let’s talk now about which things in the universe grow exponentially.
The first one, we already know, is the spreading of an infectious disease. Viruses and bacteria, if left alone, grow exponentially. Infection is a mechanism of reproduction, in which each individual gives birth to a few individuals who, in time, will give birth to some new individuals.
That’s why animals also obey the law of exponential growth: they reproduce, that is, make little copies of themselves with the ability to make new copies. If nothing slows them down, you have rabbits in Australia, for example. Or, according to Agent Smith, humans.
Not the only thing that grows exponentially. Compound interest also grows exponentially. Compound interest is achieved in a very simple way: if you put away a savings account of, say $1,000 which pays interest annually, you’ll see that after a few years you’ll have much more money than when you began. For example, for $1,000, 10% interest and 60 years you’ll end up with $304,488. That’s a nice way to become rich, right?
Wrong. Despite what many people say about the wonders of compound interest, it simply doesn’t work. There’s another force at play here that also grows exponentially and it’s much more relentless: inflation. Inflation is also an exponential growth. Money has lost half of its value since 1990 and that usually erases any expectations about compound interest.
Viruses, bacteria, inflation… Is there any exponential growth that does some good? Well, there’s Moore’s law.
In 1965, Gordon Moore, CEO of Intel, noticed that computer science was advancing really fast. Moore observed that the number of transistors in microprocessors doubled every two years. It’s been true since then.
There are other things that have been growing exponentially in the computer realm. For example, the number of mobile phones in the world until 2012, the price of Apple shares or the amount of information generated by mankind.
This last one is a good example of how far the origin looks when you are riding an exponential wave. 90% of all the information generated by mankind has been created in the last 24 months. That includes all of the classics: movies, books, games and TV shows. (remember, we’re talking about the quantity of information, not its quality).
Another fact: the inhabitants of the city of Alexandria produce every second as much information as the mythical library of Alexandria had during its peak. (The mythical library of Alexandria had almost half a million books. If we calculate 20 MB per book, it’s about 10 TB. Every human being in 2020 produces around 1.7 MB per second, which is roughly 10 TB for the 5,200,000 inhabitants in Alexandria.)
But there’s one caveat. Halfway through the chessboard there was no more rice in the kingdom. Moore’s law is probably reaching its end. After 100 exponential paces there’s no more universe to roam. Apple shares are no longer growing exponentially. That’s right, we’ve found a pattern: exponential growth cannot be held infinitely in the real world.
Usually, after a period of exponential growth we can see a flattening of the curve, which then begins to look like an S. Good news in the case of virus and bacteria, but not for other things. For example, in the case of Moore’s law it means that we have to look elsewhere if we want to keep on growing in knowledge and abilities. And we do want to keep on growing.
Are there any places where the exponential growth never ends? Well, buckle up because things are gonna get weird.
We have seen that in the real world there’s no room for a really extended exponential growth, but that depends on what you call the real world. There’s a place where the exponential function grows indefinitely, and that’s the realm of possibilities.
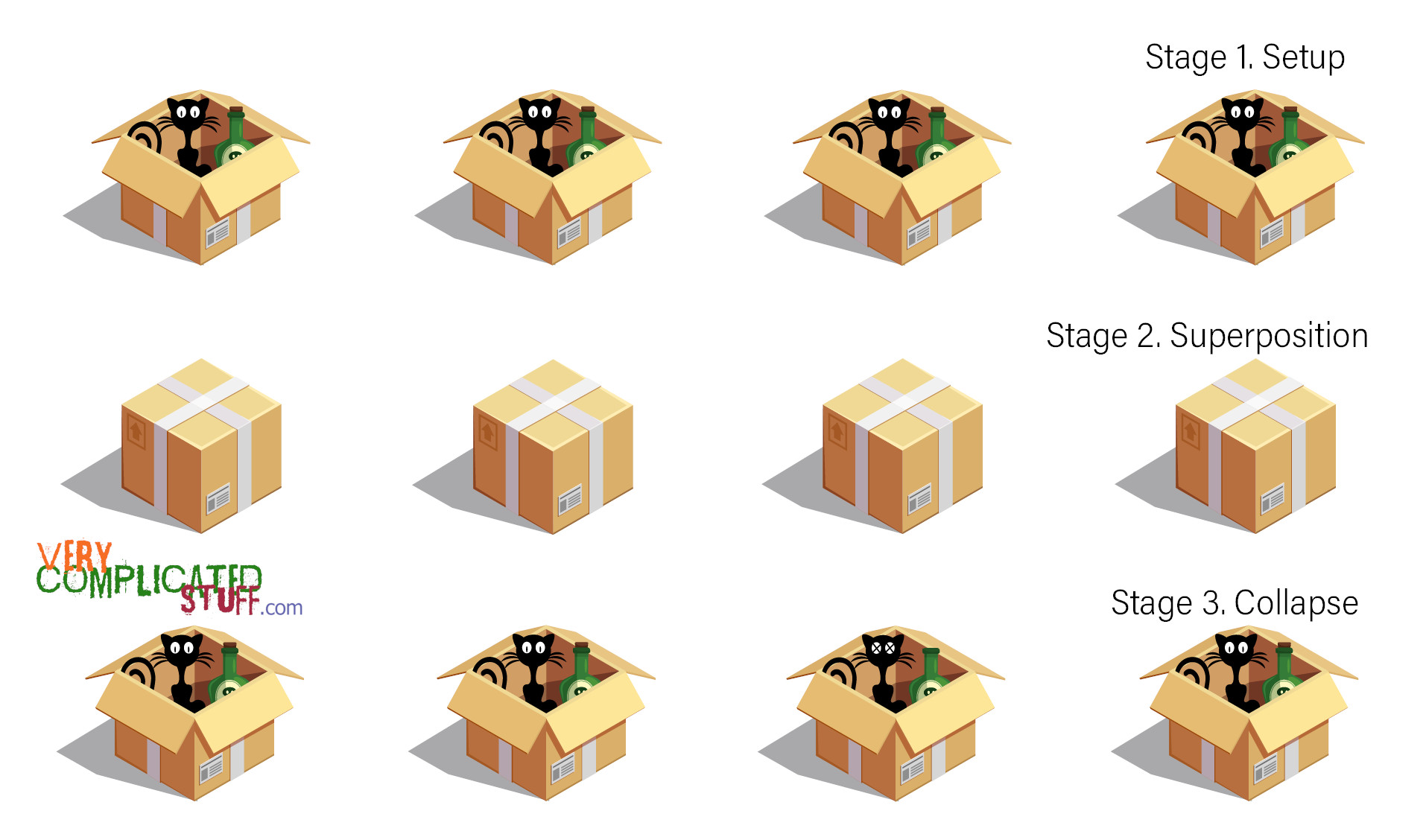
Let’s observe the Schrödinger’s cat (we will call her Schrö from now on). We’ll put her inside an evil contraption that decides her fate according to the state of a subatomic particle. While we don’t look, the cat is half alive and half dead, but when we look, we find out.
That’s called a superposition of states, being half alive and half dead.
Let’s put another contraption with another cat (we’ll call her Schrö Schrö). When both cats are half dead, half alive, they have a total of four possibilities. Let’s count them: Scrhö alive, Schrö Schrö alive; Schrö dead, Schrö Schrö dead; Schrö alive, Schrö Schrö dead and Schrö dead, Schrö Schrö alive.
Yes, that’s four.
What if we add another cat? You guessed it, we’ll have 8 possibilities. 4 cats? 16 possibilities. And so on and so forth.
Let’s stop on four cats. Let’s open their boxes. In that moment the sixteen possible states collapse into one and the other fifteen are discarded. In the image above, the superposed estates collapse in one of the cats (Schrö Schrö Schrö) dead and the rest alive. We have chosen a reality among sixteen possibilities. But have we?
(Note: No actual cats were harmed during this thought experiment).
Maybe all the possibilities are real and the universe splits into sixteen universes, each of them with a different outcome. Yes, parallel worlds. Maybe time is just the path we’re walking between parallel worlds.
But let’s for a moment calculate how many parallel worlds there could be. There are a lot of things in the universe, but let’s look only at the atoms. Each and every atom in the universe has different states, all of them superposed. There are 1080 atoms in the universe, give or take a few. That’s equivalent to 1080 cats in our thought experiment.
If each particle had only 2 states, that would imply

possible universes. Remember that the radius of the whole observable universe was about 2100, so don’t get lost on one of them, maybe you won’t be able to return.
Finally, let’s add time to the equation. Because those states are per unit of time. And there are a lot of units of time.
Do you feel closer to the infinite yet?